在统计分析中,t分布是小样本数据推断的核心依据,而WPS表格中的TDIST函数,正是快速计算t分布概率的高效工具。无论是学术研究中的显著性检验,还是商业决策里的差异分析,TDIST函数都能凭借对t分布的精准解析,让复杂的概率计算变得简单可控。掌握TDIST函数,不仅能提升统计分析的效率,更能为基于t分布的数据分析提供可靠支撑。
一、TDIST函数的基础解析
1.函数语法与参数
TDIST函数的语法为:TDIST(x,degrees_freedom,tails),三个参数的核心含义如下:
- x:需计算概率的t值,必须为正数(若为负数,可利用t分布对称性取绝对值,结果不变)。
- degrees_freedom:自由度(样本量n-1),需为大于0且小于10^10的整数,反映样本中独立信息的数量。
- tails:尾部数量,仅能取1(单尾概率)或2(双尾概率),分别对应“t值大于x”或“t值绝对值大于x”的概率。
例如,t值为1.833、自由度为9时,TDIST(1.833,9,1)返回单尾概率约5%,TDIST(1.833,9,2)返回双尾概率约10%,与t分布表结果完全一致。
2.核心特性
适用场景:专为小样本(n<30)设计,当总体标准差未知、需用样本标准差替代时,数据服从t分布,此时TDIST函数尤为适用。
与正态分布的关联:自由度增大时,t分布趋近于标准正态分布(如自由度=100时,两者差异极小)。
二、TDIST函数的实战应用
1.基础概率计算
只需在WPS表格中输入公式,即可快速得到结果。例如:
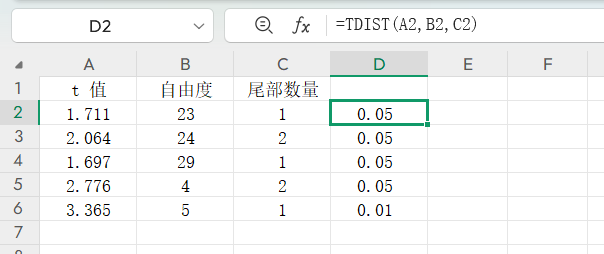
对于t值2.064、自由度24、双尾检验,TDIST(2.064,24,2)返回约5%,表示t值绝对值大于2.064的概率为5%。
对于t值3.365、自由度5、单尾检验,TDIST(3.365,5,1)返回约1%,对应更严格的显著性水平。
2.典型分析场景
单样本t检验:验证样本均值与总体均值的差异。如某零件标准直径10mm,25个样本均值10.2mm、标准差0.5mm,计算得t值=2,自由度=24,双尾概率TDIST(2,24,2)≈5.6%,因大于5%的显著性水平,可判断无显著差异。
两独立样本t检验:比较两组数据均值差异。如A、B两种教学方法的学生成绩,计算得t值=2.83、自由度=36,双尾概率TDIST(2.83,36,2)≈0.7%,因小于5%,可判断方法效果有显著差异。
三、常见错误与使用技巧
1.错误处理
- #NUM!错误:多因x为负数(解决:用ABS(x)取绝对值)、自由度非正整数(解决:检查样本量计算)或tails非1/2(解决:按检验类型修正)。
- 结果偏差:若与查表结果有细微差异,多因t值精度不足,可保留更多小数位(如1.711改为1.710882)。
2.实用技巧
结合IF函数自动判断显著性:如=IF(TDIST(x,df,2)<0.05,"显著","不显著"),可批量处理检验结果。
动态计算自由度:用COUNTA(数据区域)-1替代手动输入,样本量变化时自动更新(如TDIST(t值,COUNTA(A2:A26)-1,2))。
结语
WPS表格中的TDIST函数,以简洁的语法和精准的计算,成为t分布分析的得力助手。无论是小样本的假设检验,还是差异显著性的快速判断,它都能让复杂的统计计算变得高效可控。掌握TDIST函数,不仅能提升数据分析的效率,更能让基于t分布的决策更具科学性——让这个工具成为你统计分析中的实用利器,让数据洞察更精准、更高效。









评论 (0)