在数据驱动决策的时代,理解数据的离散程度是挖掘数据价值的关键,而标准差正是衡量这一特征的核心指标。无论是分析学生成绩的波动、评估投资风险,还是监测产品质量的稳定性,标准差都能提供直观参考。在WPS表格中,STDEV函数是计算标准差的高效工具,掌握STDEV函数、用好STDEV函数,能让复杂的数据处理变得简单高效。
一、STDEV函数基础:语法与操作
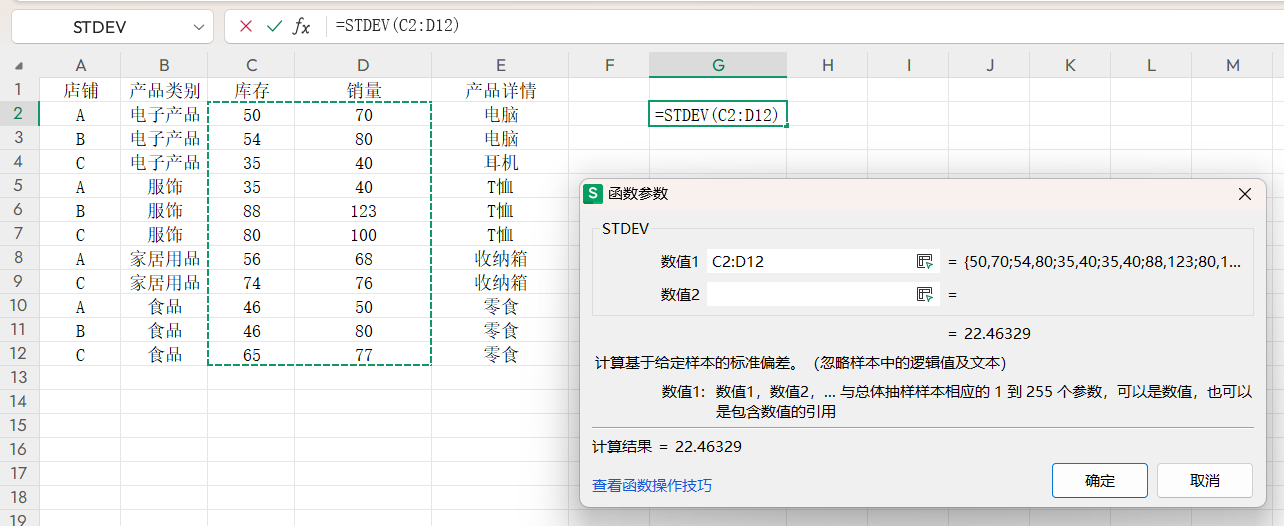
STDEV函数用于计算样本数据的标准差,基本语法为STDEV(number1,number2,...)。其中,number1是必需参数(可为数值或单元格引用),number2,...为可选参数(最多29个)。若数据在连续单元格区域(如C2:D12),直接用=STDEV(C2:D12)更简洁,尤其适合大量数据处理。
操作步骤仅需三步:选中结果单元格→输入公式(确保英文状态)→回车。例如计算C2:D12的标准差,输入=STDEV(C2:D12)即可快速得出结果。
二、核心原理:样本与数据处理规则
STDEV函数的关键前提是:它计算的是样本标准差,采用“n-1”无偏估计(n为样本量),更适合通过样本来推断总体离散程度。若数据是完整总体(如全班所有学生成绩),则需用STDEVA函数(分母为n),避免结果偏差。
数据处理上,STDEV会自动忽略逻辑值(TRUE/FALSE)和文本。若需纳入这些数据(如将“优秀”视为0),需改用STDEVA,否则会因数据遗漏导致结果失真。
三、实战场景:STDEV函数的3大应用
- 教育领域:分析学生成绩分布。若一班成绩标准差小,说明分数集中、水平均衡,可侧重拓展教学;二班标准差大,提示成绩两极分化,需加强分层辅导。
- 金融领域:评估投资风险。股票收益率的标准差越大,说明收益波动越剧烈,风险越高。保守型投资者可优先选择标准差小的资产。
- 质量控制:监测产品稳定性。如零件尺寸的标准差小,表明生产精度高、质量稳定;若标准差超标,需排查设备或原材料问题。
四、避坑指南:常见错误及解决
- 参数错误:非数值数据(如“缺考”文本)会导致计算失败,需清理或转换数据格式。
- 范围错误:误选单元格区域(如A1:B10而非A1:A10)会引入无关数据,建议用鼠标拖拽选择区域减少失误。
- 函数选错:混淆样本与总体数据,误用STDEV(样本)计算总体标准差,结果会偏小,需根据数据性质选择函数。
五、总结:让STDEV函数成为数据分析利器
STDEV函数虽简单,却能在多个场景中发挥关键作用。它将复杂的标准差计算简化为公式输入,帮助快速判断数据波动。无论是教师、投资者还是质检人员,掌握其语法、原理及避坑技巧,就能让数据离散程度的分析更高效、结论更可靠。用好STDEV函数,让每一组数据都能为决策提供精准支撑。









评论 (0)