在数据驱动决策的时代,我们常被各类数据关系困扰:学习时长与成绩是否正相关?广告投入能否直接拉动销量?这些问题的答案,藏在数据的相关性中。而WPS中的PEARSON函数,正是解锁这类关系的关键工具,PEARSON函数能精准计算变量间的线性相关程度,为分析提供可靠依据。无论是学习、工作还是研究,PEARSON函数都是不可或缺的数据分析助手。
一、PEARSON函数:线性相关的“测量尺”
PEARSON函数全称皮尔逊乘积矩相关系数函数,核心是计算相关系数r,以此衡量两组数据的线性关联强度:
- 当r接近1时,为强正相关(如投入增加,产出上升);
- 当r接近-1时,为强负相关(如价格上涨,销量下降);
- 当r接近0时,几乎无线性相关(如降雨量与手机销量)。
其语法结构简洁:=PEARSON(array1,array2)。其中,array1为自变量(如学习时间),array2为因变量(如成绩),两者需为同长度的数值集合(文本、逻辑值会被忽略,数据量不同则返回#N/A错误)。
二、WPS中PEARSON函数的使用步骤
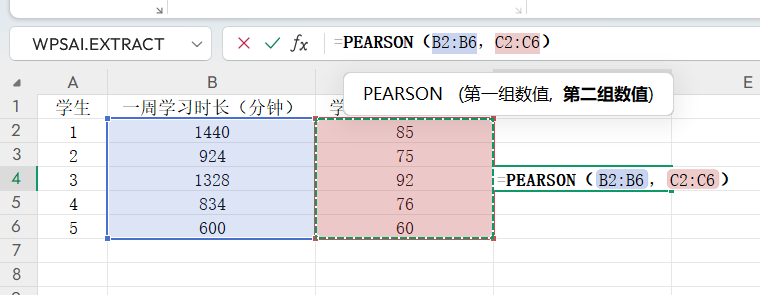
- 准备数据:确保两组数据准确完整,格式统一为数值(避免文本干扰)。例如,B列存5名学生的每周学习时长,C列存对应成绩。
- 插入函数:选中结果单元格(如D3),点击“插入函数”,在“统计”类别中选择“PEARSON”。
- 填写参数:输入array1(如B2:B6)和array2(如C2:C6),确保数据长度一致。
解读结果:数据返回r=0.9,说明学习时长与成绩呈强正相关
三、跨领域应用:PEARSON函数的实战价值
- 教育领域:分析学习方法与成绩的关系。若某班级“错题整理次数”(A列)与“考试分数”(B列)的r=0.7,说明错题整理对成绩提升有显著正向作用,可据此优化学习策略。
- 市场营销:评估广告投入(A列)与销售额(B列)的关联。若r=0.65,表明广告对销量有中度拉动作用,企业可针对性增加高转化渠道的投放。
- 金融分析:研究股票价格(A列)与成交量(B列)的关系。若r=0.5,说明价格波动与交易活跃度存在一定正相关,可辅助判断市场趋势。
- 医学研究:探究药物剂量(A列)与疗效指标(如血压下降值,B列)的关联。若r=-0.7,表明剂量增加与疗效提升呈强负相关(如降压药剂量越高,血压降得越多),为用药方案提供参考。
四、与同类函数的区别:选对工具更高效
- 与CORREL函数:两者功能几乎一致,均计算皮尔逊系数,仅名称不同,实际使用中可互换。
- 与RSQ函数:RSQ返回拟合优度的平方(0-1之间),侧重评估线性回归模型的拟合效果;PEARSON则直接反映线性相关的强弱与方向,前者是“模型评估”,后者是“关系判断”。
- 与协方差函数(COVARIANCE.P/S):协方差受量纲影响(如“元”与“千克”无法直接对比),而PEARSON通过标准化处理,结果在-1到1之间,更易直观解读。
五、使用须知:避开这些“坑”
数据质量是前提:异常值(如错填的极端值)和缺失值会严重影响结果,需提前清洗(如删除异常值、用均值填充缺失值)。
相关≠因果:若冰淇淋销量与溺水人数的r=0.8,并非前者导致后者,而是两者均受“高温”影响。分析时需结合业务逻辑,避免误判。
总结:让数据说话的关键一步
PEARSON函数的核心价值,在于用数据量化变量关系。掌握它,既能在工作中优化资源投入(如广告、学习时间),也能在研究中发现潜在规律。在WPS中熟练运用PEARSON函数,让每一组数据都成为决策的“指南针”。









评论 (0)