GEOMEAN返回一组正数数据或正数数据区域的几何平均值,注意是正数数据,只要任意一个数字是负数都将会报错。
我们平常提到的求平均值,指的是算数平均值,比如x1,x2,...xn的算数平均值是
x=(x1 x2 ... xn)/n
而几何平均值的定义函数为GM=
我们先看一下函数法求几何平均值
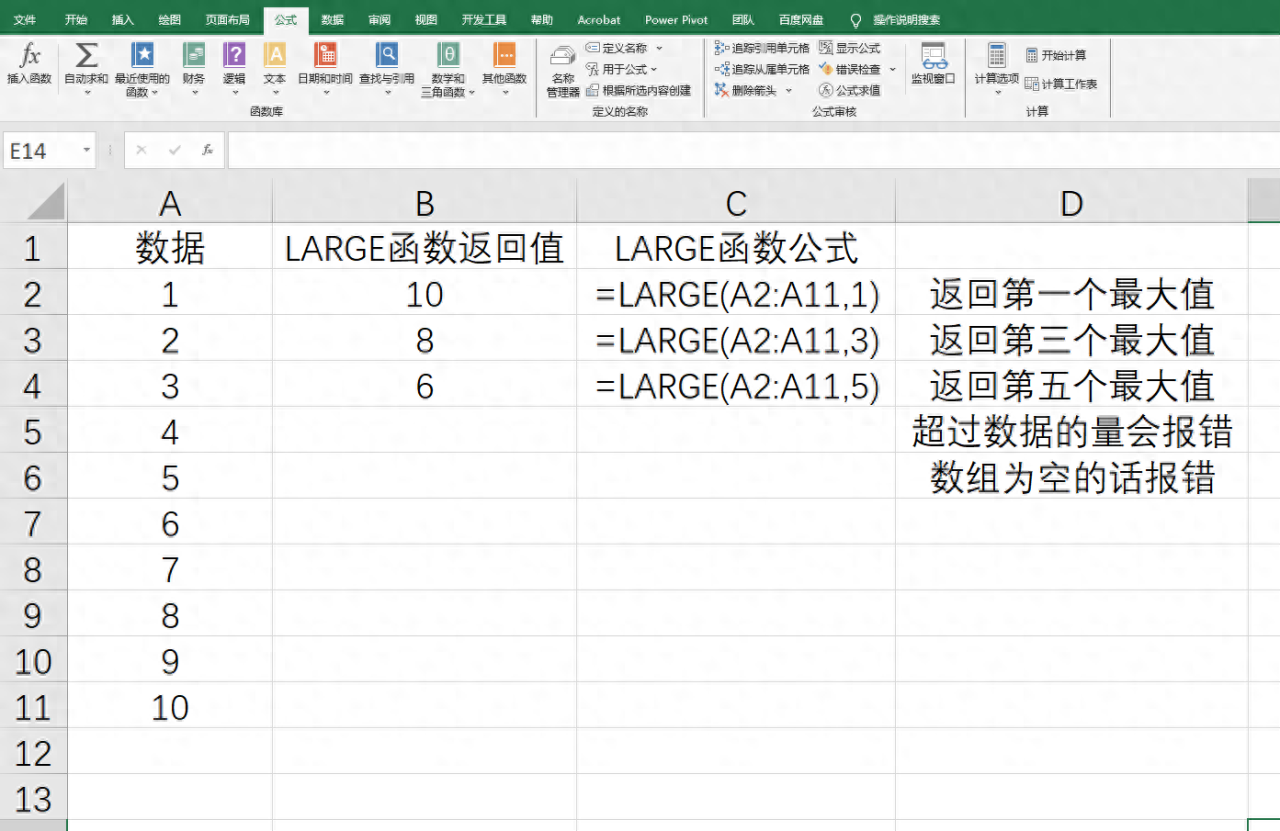
| x | 函数返回值 | 函数表达式 |
| 1 | 4.528728688 | =GEOMEAN(A2:A11) |
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 | ||
| 10 |
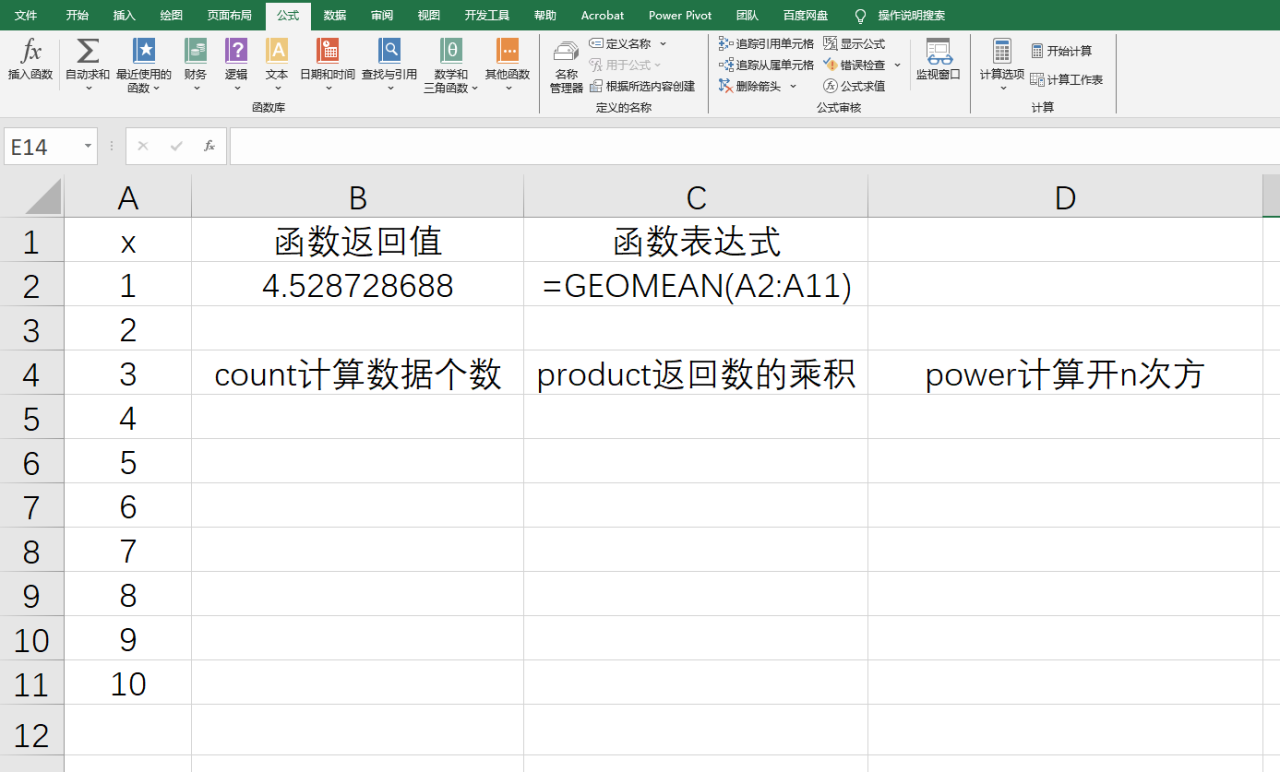
再看一下按照公式计算出来的几何平均值
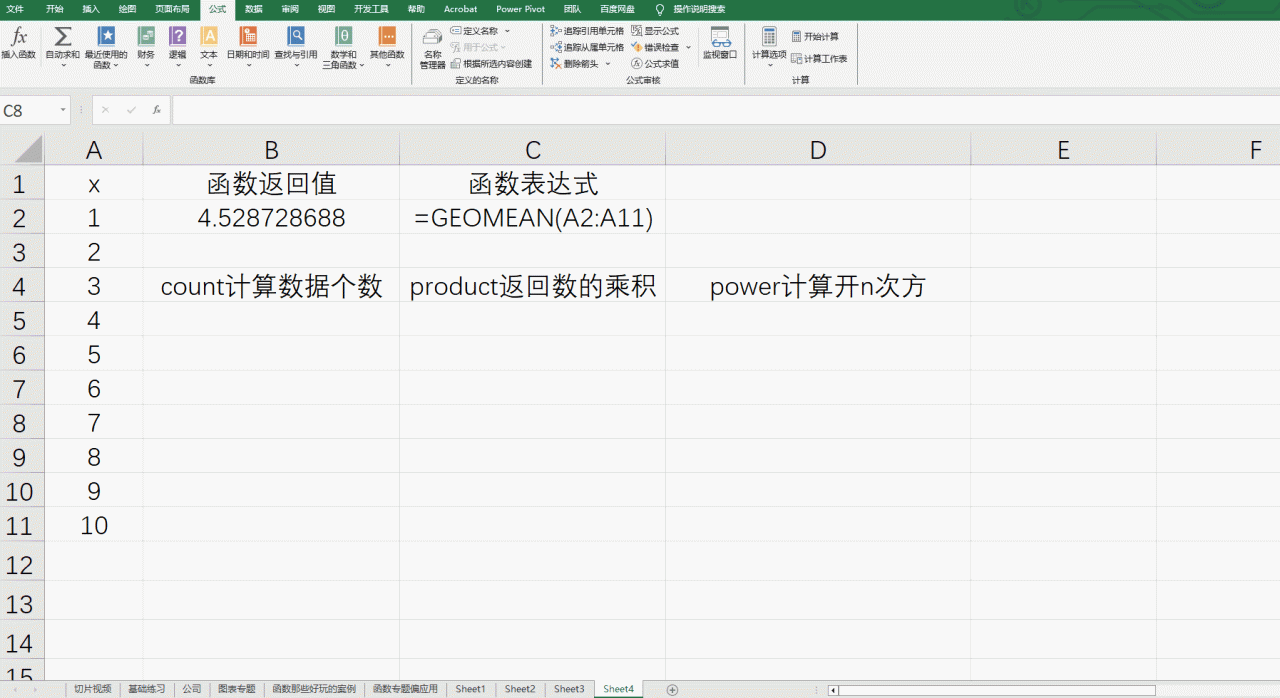
| x | 函数返回值 | 函数表达式 | |
| 1 | 4.528728688 | =GEOMEAN(A2:A11) | |
| 2 | |||
| 3 | count计算数据个数 | product返回数的乘积 | power计算开n次方 |
| 4 | 10 | 3628800 | 4.528728688 |
| 5 | =COUNT(A2:A11) | =PRODUCT(A2:A11) | =POWER(C5,1/B5) |
| 6 | |||
| 7 | |||
| 8 | |||
| 9 | |||
| 10 |
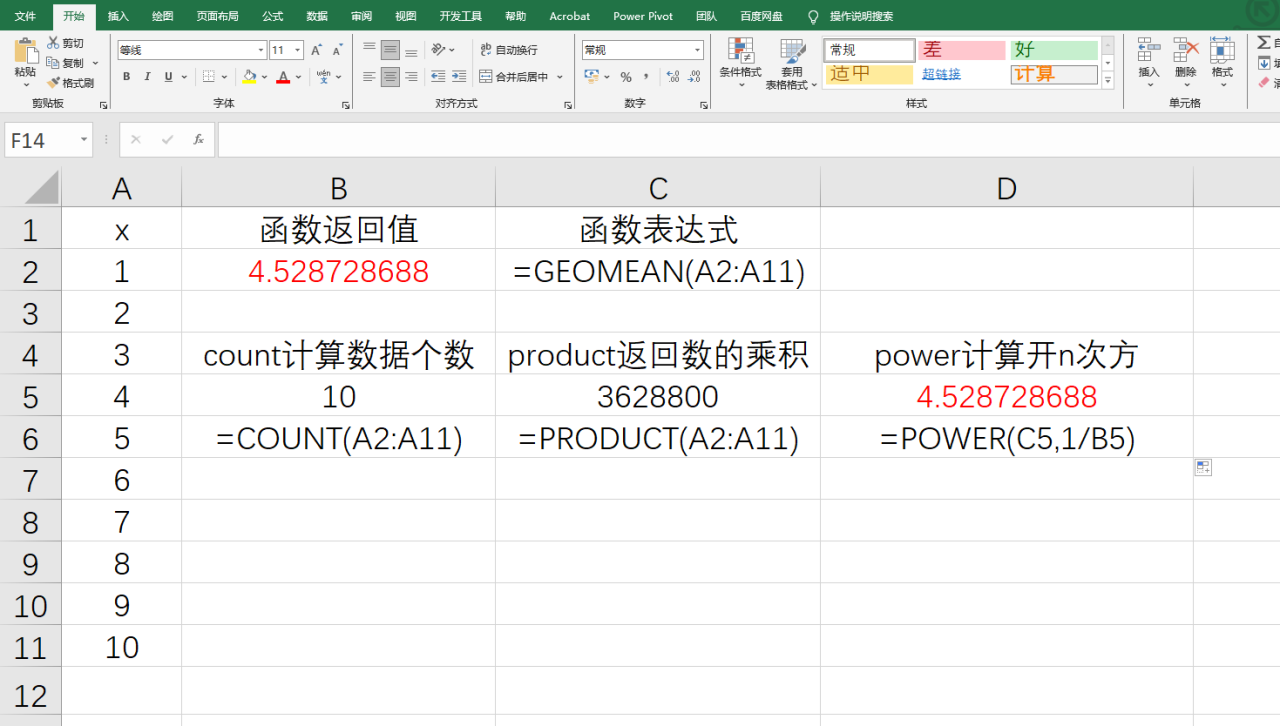
从上面的过程可以看出来,GEOMEAN几何平均值函数直接计算出几何平均值过程比较简单,当然通过公式计算出来的结果尽管繁琐,但是它有各种的过程量,只要你会过程不知道这个函数也没关系。
函数创造出来,本质上是为了简化我们的工作或者方便我们的工作,应该根据具体的场景需要选择合适的方式。









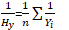
评论 (0)