提到单变量求解,不少人会被“根据公式目标值反推变量取值”的专业解释绕晕;其实单变量求解本质是Excel里的“解方程神器”,新手也能快速上手;今天就用大白话拆解单变量求解,帮你彻底搞懂它的用法。
一、单变量求解作用
专业定义里的“目标单元格、目标值、可变单元格”,翻译过来就是我们熟悉的方程要素。
比如已知Y=ax+b,且Y=P,求X的过程,就是单变量求解的核心逻辑——固定方程结果,反推其中一个未知数的取值。
简单来说,它帮我们省去手动计算的麻烦,一键算出公式中未知变量的具体数值。
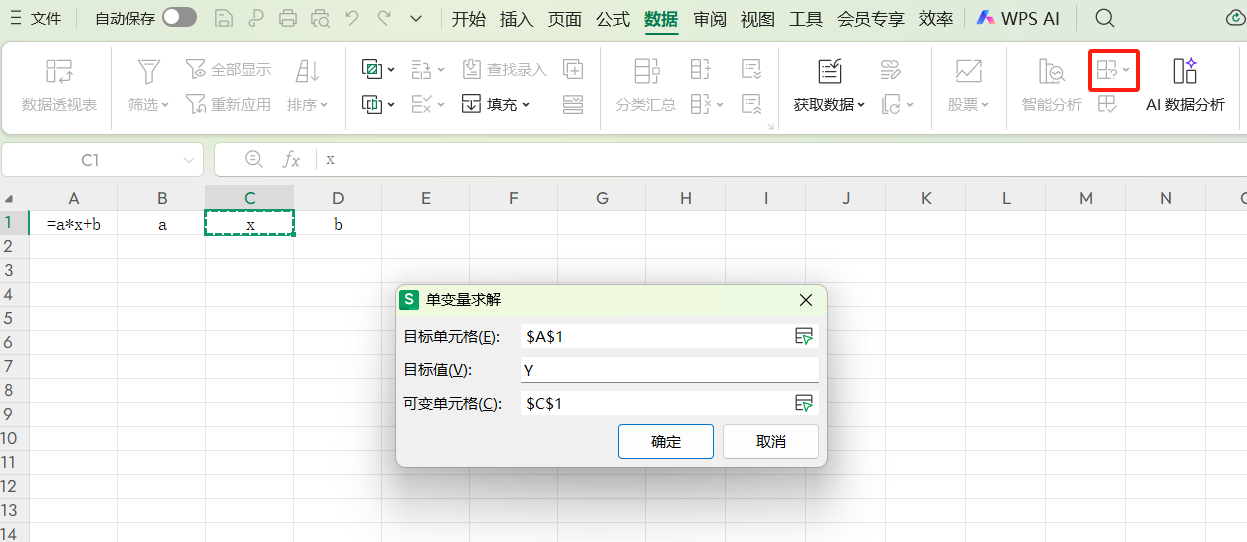
二、核心参数
无论复杂与否,单变量求解都围绕三个参数运转,记住它们就能找准操作核心:
- 目标单元格:对应方程的“表达式”,比如Y=aX+b中的Y,是存放公式的单元格;
- 目标值:对应方程的“结果”,即例子中的P,是我们希望公式得到的具体数值;
- 可变单元格:对应方程的“未知数”,也就是需要求解的X,是公式中可变动的变量单元格。
三、实操步骤
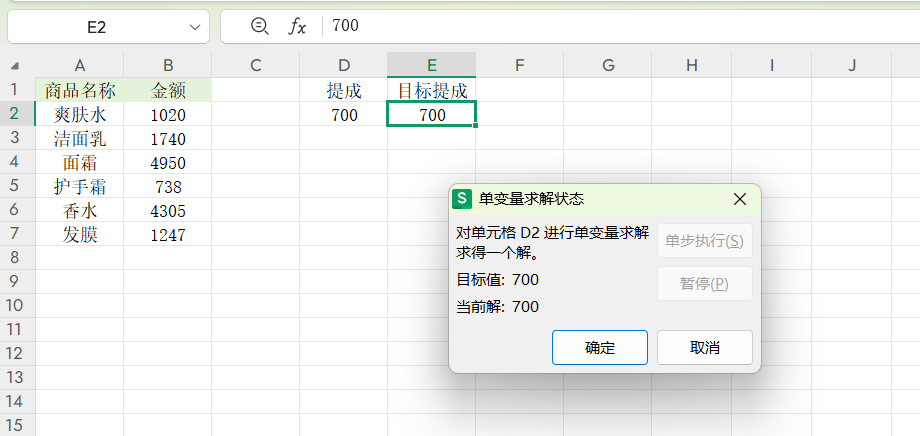
单变量求解只需三步,以业务员销售提成为销售业绩总和的5%,想得到700元的提成,发膜需要多少销售额为例:
1.提成=销售总额×5%,公式为=SUM(B2:B6)*0.05
2.确定参数:目标单元格选提成所在单元格,目标值设为700元,可变单元格选择B7;
3.启动求解:通过“数据—模拟分析—单变量求解”路径,填入上述参数后点击确定,Excel会自动迭代计算出结果。
4.得出结果:若想拿到700元提成,发膜销售额需达到1247元。
结语
其实单变量求解的核心就是“结果反推变量”,无论是计算销售目标、还款金额还是成绩达标线,只要符合“单方程单未知数”的场景,它都能派上用场。掌握这个小工具,能帮你在数据处理中少走很多弯路。









评论 (0)