在数据分析中，了解数据分布形态至关重要，而WPS中的SKEW函数正是揭示数据分布特征的实用工具。无论是判断数据是否对称，还是发现潜在的极端值，SKEW函数都能提供关键参考。掌握SKEW函数的使用方法，能让我们更精准地解读数据背后的规律。

一、SKEW函数核心概念

SKEW函数即偏态系数函数，用于衡量数据分布的不对称程度。它通过计算数据与平均值的偏差，输出一个数值反映分布形态：

  • 结果=0：数据接近对称分布（如理想状态下的掷硬币次数统计）
  • 结果>0：右偏态分布（多数数据集中在左侧，存在少数极大值）
  • 结果<0：左偏态分布（多数数据集中在右侧，存在少数极小值）

其现实意义在于提前洞察数据“性格”：电商通过它发现用户消费分层，教育者用它定位学生成绩短板，这些分析都能直接指导决策。

二、SKEW函数使用指南

（1）基础语法

公式结构：=SKEW(number1,[number2,...])

number1：必需参数（数值或单元格区域）

[number2,...]：可选参数（最多255个）

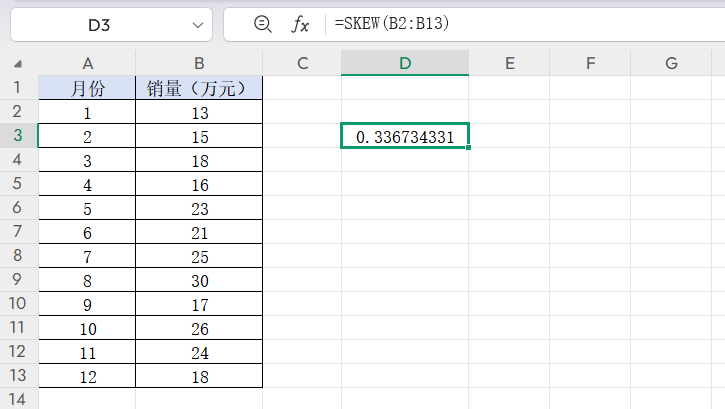
示例：计算B2到B13的数据偏态，输入=SKEW(B2:B13)即可。

WPS表格进阶必学！SKEW函数使用指南-趣帮office教程网

（2）使用注意

仅支持数值型数据，文本、逻辑值会被自动忽略

建议使用连续单元格区域（如A1:C100），减少参数输入错误

样本量越大，结果越可靠（小样本易受随机因素影响）

三、实战场景与进阶技巧

（1）典型应用场景

  • 市场调研：分析产品满意度评分，右偏需关注负面评价原因
  • 财务分析：应收账款账龄右偏时，需加强长期账款催收
  • 教学管理：作业完成时间左偏，可适当增加作业难度

（2）函数联动技巧

  • 与AVERAGE结合：平均值高但SKEW右偏，说明少数极值拉高整体水平
  • 与IF搭配：=IF(SKEW(A1:A10)>0,"右偏","正常/左偏")，实现数据自动分类

结语

SKEW函数虽简单，却能成为数据分析的“透视镜”。它帮助我们跳出“平均值陷阱”，从分布形态中发现关键信息。无论是商业决策还是日常数据处理，善用SKEW函数，就能让每一组数据都发挥最大价值，让分析更精准、决策更科学。