在数据驱动的时代,精准分析数据特征离不开对离散程度的把握,而标准差正是描述数据波动的核心指标。在WPS表格中,STDEV.P函数是计算总体标准差的高效工具,但很多人因混淆STDEV.P函数与其他函数而导致结果偏差。今天,我们就来系统学习STDEV.P函数,让它成为数据处理的得力助手。
一、STDEV.P与STDEV:别再弄混这两个函数
STDEV.P函数的核心作用是计算总体标准差,反映整个研究对象的离散程度;而STDEV函数用于计算样本标准差,适用于从总体中抽取的部分数据。二者最关键的区别在于计算逻辑:
- STDEV.P假设数据是完整总体,用“n”(数据个数)作为自由度;
- STDEV假设数据是总体样本,用“n-1”作为自由度。
例如:若分析一个班级30名学生的成绩(该班级即研究总体),必须用STDEV.P;若该班级是全校学生的样本,则应使用STDEV。这个区别看似细微,却可能导致结果显著偏差。
二、STDEV.P函数的使用方法
函数格式为STDEV.P(number1,[number2],...)
- number1:必需参数,首个总体数据(可直接输入数值或引用单元格区域);
- [number2],...:可选参数,最多254个其他数据。
示例:
直接输入数值:STDEV.P(85,90,95,80,75)
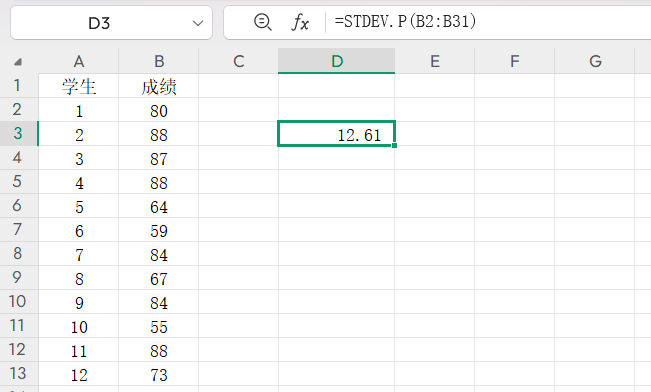
引用单元格:STDEV.P(B2:B31)(计算B2到B31的总体标准差)
注意:引用区域需排除无关数据,避免结果失真。
三、STDEV.P的实际应用场景
- 教育领域:评估成绩稳定性
某老师分析两个班级的数学成绩,用STDEV.P计算得:一班标准差为7,二班为14。那就说明一班成绩更均衡,二班两极分化明显,可据此制定针对性教学方案。
- 企业管理:监控绩效波动
某公司20名销售人员的月度绩效得分存于C1:C20,用STDEV.P(C1:C20)算出标准差6。若较上月的9下降,说明绩效更稳定,团队水平在提升。
- 生产制造:把控产品质量
电子厂检测100个电阻的阻值(存于D1:D100),用函数算出标准差2.1Ω,若在规定范围(≤2.5Ω)内,说明生产稳定;超范围则需排查设备或原料问题。
- 金融行业:衡量投资风险
某投资者5只股票的年化收益率为12%、8%、15%、-3%、10%,用函数计算标准差6.8%。通过对比不同组合的标准差,可选择匹配自身风险承受能力的投资方案。
四、避坑指南:常见错误及解决方法
在使用STDEV.P函数时,有几个常见错误需要特别注意,提前规避能让计算结果更精准。
1.混淆总体和样本,用错函数。若未明确数据属性,如将班级成绩(总体)误用STDEV函数,或抽样产品数据(样本)误用STDEV.P函数,计算结果将不准确。正确做法是:数据为完整研究对象(如公司全体员工、班级全体学生),使用STDEV.P;若为总体抽样(如抽测100个产品),则使用STDEV。
2.参数混入非数值数据导致结果偏差。STDEV.P函数会自动忽略文本(如“缺考”“未达标”)和普通逻辑值(TRUE、FALSE),但经常被忽视。例如统计成绩时,含“缺考”文本的单元格会被跳过,若该数据应纳入总体,将减少计算数量、造成结果失真。解决办法:输入数据时避免在数值区域添加非数值内容;特殊情况(如“缺考”按0分计),需先将文本转为对应数值再计算。
3.数据个数不足,导致函数返回错误值。当输入的数值少于2个时,STDEV.P会返回#DIV/0!错误——这是因为标准差衡量的是数据波动,单个数据不存在“波动”的说法,至少需要2个数据才能计算。所以使用前要确保参数中至少有2个数值;如果确实只有1个数据,就没必要计算标准差了。
五、函数搭配:让分析更全面
- 与AVERAGE搭配:平均值反映集中趋势,标准差反映离散程度。例如一班平均分85、标准差8.5,二班平均分82、标准差5.3,可直观对比“整体水平”与“稳定性”。
- 与MAX、MIN搭配:结合最大值、最小值,能同时分析数据的波动范围和离散程度。如某产品尺寸最大值105mm、最小值95mm、标准差2.3mm,可判断质量稳定性。
- 与IF搭配:用数组公式STDEV.P(IF(A1:A50="一班",B1:B50))(按Ctrl+Shift+Enter确认),可计算特定条件下的总体标准差(如“一班”成绩)。
结语
STDEV.P函数虽简单,却能在教育、企业、制造、金融等领域发挥关键作用。只要明确“总体数据用STDEV.P,样本数据用STDEV”的核心原则,避开参数格式、数据量等常见陷阱,就能精准把握数据波动规律。掌握这个工具,让你的数据分析更高效、决策更科学。









评论 (0)