在数据分析过程中,计算平均增长率是一项极为常见且重要的任务。比如我们要分析某企业连续 6 年的业务增长情况,或是评估一项投资在 6 年间的收益变化,这时候就需要精准计算平均增长率。在Excel里,仅需一个简单公式就能搞定,那就是=GEOMEAN(1+B2:B6)-1 。
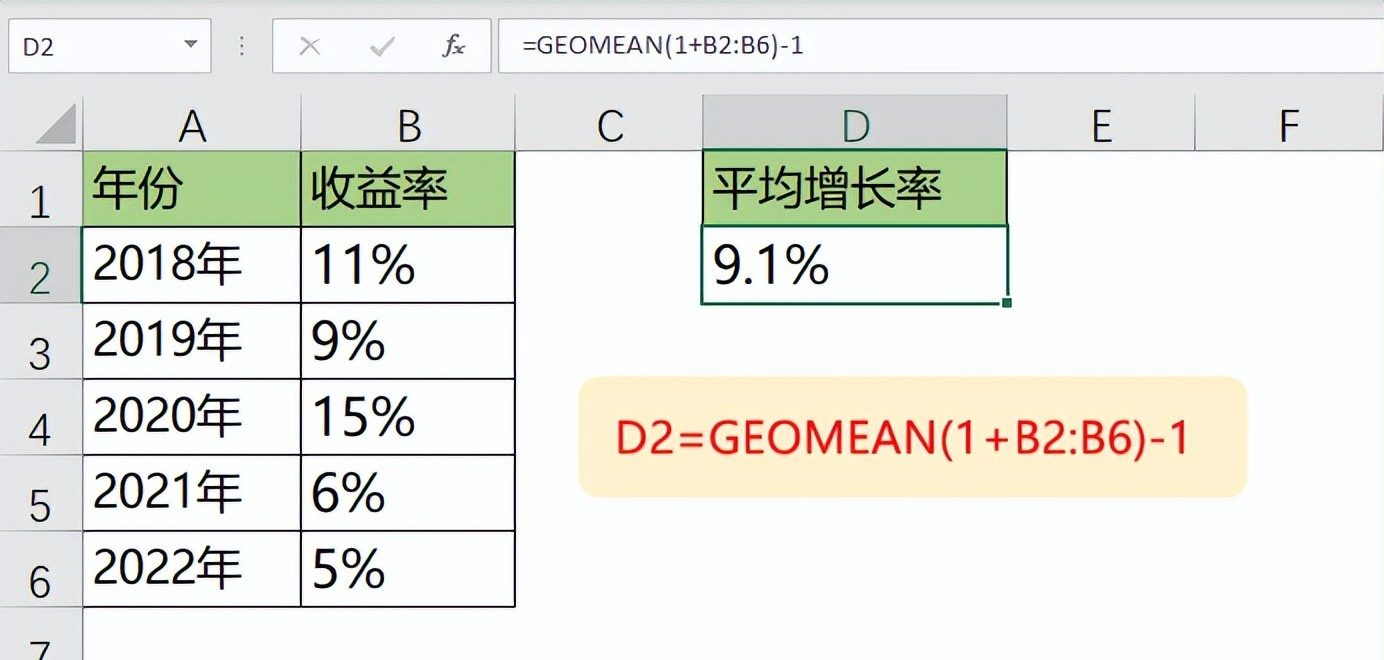
公式原理剖析
1+B2:B6:构建本利比例
假设 B2 到 B6 单元格存储的是每年相对于上一年的增长率数据(以小数形式呈现,例如 0.1 代表 10% 的增长率)。将 1 与每年的增长率相加,其意义在于得到每年的本利比例。打个比方,若某一年增长率为 0.2(即 20%),那么1 + 0.2 = 1.2,这 1.2 就意味着当年的数据量是上一年的 1.2 倍,也就是本利比例。通过这种方式,我们将每年的增长率数据转化为了便于后续计算的本利比例数组。
GEOMEAN:求取几何平均值
GEOMEAN函数在此发挥关键作用,它专门用于计算几何平均值。对于一组正数,其几何平均值的计算逻辑与普通算术平均值有所不同,它更侧重于数据间的连乘关系。在计算平均增长率的情境下,这种特性使得计算结果更能精准反映数据在一段时期内的真实平均增长态势。在公式=GEOMEAN(1+B2:B6)-1中,GEOMEAN(1+B2:B6)就是对由1+B2:B6生成的本利比例数组进行几何平均值的计算。
-1:还原为平均增长率
完成几何平均值的计算后,为何还要减去 1 呢?原因在于前面计算得到的几何平均值本质上是本利比例的平均值,并非我们最终想要的平均增长率。减去 1 这一步,就是将以本利比例平均值形式呈现的结果,转换回我们所熟悉的增长率形式。例如,当计算出的几何平均值为 1.15 时,1.15 - 1 = 0.15,即得出平均增长率为 15% 。
应用场景示例
假设有一家电商企业,统计了近 6 年的年度销售额增长率,数据存放在 B2 到 B6 单元格。
| 年份 | 销售额增长率(小数形式) |
|---|---|
| 第 1 年 | 0.08 |
| 第 2 年 | 0.12 |
| 第 3 年 | 0.05 |
| 第 4 年 | 0.10 |
| 第 5 年 | 0.15 |
| 第 6 年 | 0.09 |
在需要得出平均增长率的单元格(如D2)中输入=GEOMEAN(1+B2:B6)-1,按下回车键,Excel 便会依序执行公式的各个步骤,最终在D2单元格呈现出该电商企业这6年销售额的平均增长率。

无论是企业管理者分析业务发展趋势,还是投资者评估企业投资价值,掌握这一计算平均增长率的方法,都能让数据解读更加高效、决策依据更加可靠。









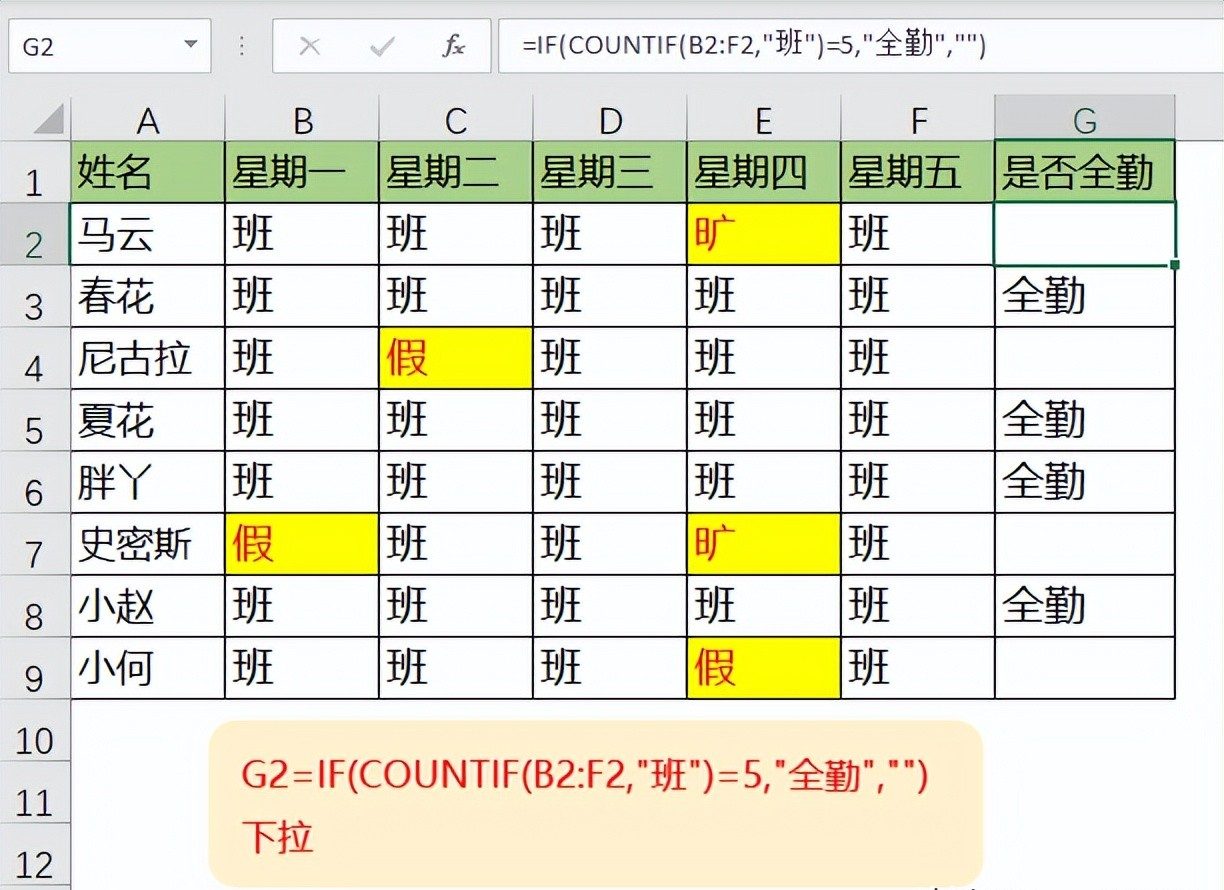
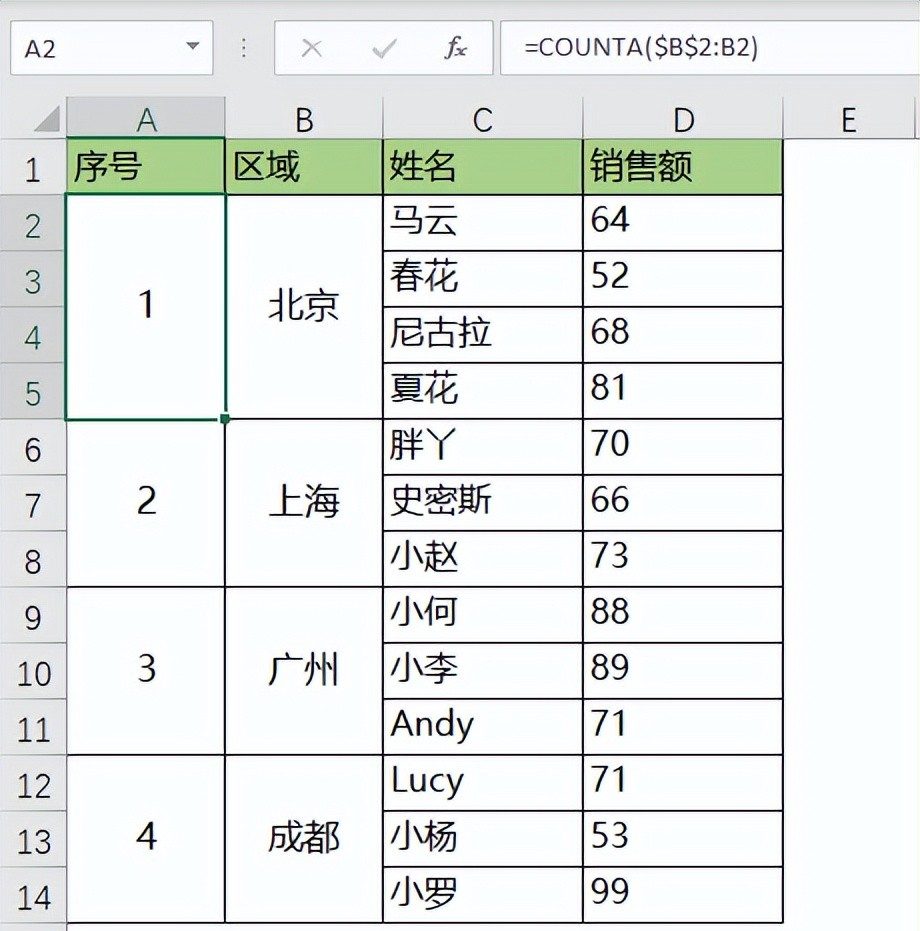
评论 (0)